Competitive. Fiery. Passionate.
Cheater.
Dirty.
Grayson Allen has been called many things during his four-year career at Duke, but there’s no denying that the 6-foot-4 guard could play basketball.
Allen first burst onto the national scene during his freshman year doing things like this:
And like this, during the NCAA Championship Game, where he became every Duke fan’s hero:
From then on, it was clear that Allen’s future with Duke was going to be bright. Returning for his sophomore year, and finally logging starter minutes, Allen put up gaudy numbers in the competitive ACC. Playing shooting guard, Allen upped his scoring average to 21.6 points per game and was shooting a blistering 41.7 percent from 3. Playing with two future first-round draft picks in Brandon Ingram and Luke Kennard, Allen showed scouts he was also first-round material.
His sophomore year, filled with bright spots, was unfortunately blemished by his decision-making. On the court, Grayson wasn’t the best at keeping his composure, leading to tripping incidents like this one against Louisville:
In retrospect, Allen’s biggest mistakes his sophomore season were not his on-court activities. Grayson’s biggest mistake was forgoing the 2016 NBA Draft in order to remain at Duke; he was project by DraftExpress at the time to go No. 29.
Grayson’s following seasons were not impressive. Making the move to point guard, Allen saw his scoring, shooting, and turnover rates worsen. DraftExpress projected Allen would go late in the second-round of the 2017 Draft. Because of his poor performance, Allen remained at Duke for his senior season. Allen improved his production as a senior, but he never reached the market value of his sophomore season.
Quantifying draft stock
Grayson Allen’s NCAA career brings up an interesting question that many collegiate basketball players face: “Will staying another year help, or hurt, my chances at the NBA?” It could be argued that Grayson actually made the correct decision in staying after his sophomore year, but was just hit with an unfortunate result; his draft stock could have actually risen and dropped him in the early to mid-first round of the 2017 NBA Draft.
In fact, the question we are really asking is, “if player ‘X’ has ‘Y’ NBA potential now, what will his NBA potential be next year?”. In order to really answer this question, there must be some notion of a player’s NBA potential, or NBA draft stock.
In order to come up with this idea, I’ve taken collegiate data, and built a model which outputs the probability of an individual being NBA material or not. If you want to read more about the process, you should look here. A few important variables the model looks at are displayed below, for reference:

The output probability of this model represents the individual’s draft stock.

The x-axis represents each year that Grayson played at Duke. The left-hand y-axis represents where DraftExpress marked Allen to go in that year’s draft. The right-hand y-axis represents Allen’s projected draft stock.
The draft projections very well match up with what DraftExpress suggested for Allen. We clearly see that Allen’s peak sophomore season had Allen at his highest position on the board. His transition to point his junior season saw his stock drop 30 percent. As mentioned previously, Allen’s lowered efficiency and high turnover rate contributed to his decline.
From this, it is still difficult to determine if Grayson Allen made the right decision but was plagued by unfortunate results, or if he made the incorrect decision and deserved what he got. In order to answer this question, I back-filled my training data set (does not include Grayson) with the predicted probabilities for each observation. Only looking at guards choosing to return for their sophomore season, I was met with this transition matrix:

Here, State 0 effectively means the player has between a 0-10 percent shot at the NBA, State 1 means the player has between 10-20 percent chance, and so on. The rows represent what state the player was in during his sophomore season, and the columns represent what state the player was in during his junior season after choosing to return. Keep in mind that this matrix is biased, since it excludes the players choosing to leave after their sophomore season.
Grayson was in State 6 his sophomore year, and moved to State 3 his junior year. Empirically, this should have occurred with a probability of ~9.8 percent. However, the probability of Grayson’s stock dropping or staying the same is around ~62 percent. From the data, it looks as if Grayson actually did make a bad decision.
The only way for Grayson’s decision to have been somewhat reasonable is if the ~38% chance of improving his stock was worth it or feasible.
How feasible is improving?
But what would Grayson have to do in the subsequent year to even give him a chance at improving his stock? Just purely looking at his percentile based statistics from his sophomore season (second row), there is hardly any room for improvement.
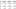
He was already topping out his Offensive Win Shares and usage, and his turnover percentage really couldn’t get any lower. Offensively, he was killing it. The only area for improvement he had was on the defensive end. More playing time at point guard his junior year wouldn’t help his rebounding or turnover numbers. Realistically, Grayson’s stock couldn’t get much higher. The poor guy had no chance.
But what if Grayson had a way to know, statistically speaking, what his stock would look like in the future? Would he be better off? In order to see whether he should have stayed, Allen could have looked at how he fared statistically his sophomore season and said “Wow, I really can’t do much better”.
Or, he could have built a model that predicts his draft stock, given previous draft stock entries.
Quantifying decisions: Building a ,odel
Give the time dependent nature of the data, I thought it be apt to apply an augmented LSTM model to predict future draft stock values. Essentially, the model looks like this:
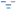
The time-series data feeds into the LSTM; the output of the LTSM is augmented with position and age to be inputted to a NN which outputs the predicted draft stock.
The model trained on all possible sequential subsets of draft stock values. For example, for a three-year player, the training data and labels would be the following: [[Year 1],[Year 1, Year 2]] and [Year 2, Year 3] respectively.
The model performed pretty poorly when only given a sequence length of one season (one-and-done). This is understandable since freshman players might play limited roles during their first year, and then experience a huge boost in playing time their sophomore years. However, with longer sequences, the model was able to predict subsequent draft stock surprisingly well.
We can use Grayson Allen again for illustration purposes.

With just one input sequence, the model does quite poorly in predicting Grayson’s sophomore year production.

With two years of information, the model does indeed predict that Allen’s stock decreases his junior year; however, it’s prediction is not as dramatic and does not expect a 30 percent dip.

With three years of prior information, the model quite successfully predicts Allen’s senior year uptick!
Obviously with more information, the model does better at determining future values. This is because the model gets a better understanding of the capabilities of a player. If it never sees high draft stock in past years, it can probably infer something about the strength of the player.
Next: Nylon Calculus: The college prospect growth curve
There are some short-comings to this model that I hoped didn’t exist. First and foremost, it predicts poorly on a sequence of length one; I was hoping this wouldn’t happen since the model would be useful in quantifying whether or not a fringe one-and-done prospect should declare. However, the model is useful for helping out with this decision for older players like Grayson.
In the future, I would like to incorporate some sort of projected conference strength and playing time variables that could help better predict those drastic changes.
And as for Grayson… he will do just fine as a second-round prospect.
