Nylon Calculus: Predicting 3-point efficiency for incoming rookies

I would like to introduce to you the greatest shooter of all-time. Andrew Tobolowsky tried to do so not long ago. Although he wrote a wonderful piece and was spot-on about me — I am, in fact, a “kid out here” and do not think he knows how to do stats because he is over 30 — he was wrong about the greatest shooter of all time.

The greatest shooter ever is Hassan Whiteside. If you doubt me, it is my honor to introduce you to Hassan Whiteside’s snapchat.

If that is not considered to be incontrovertible proof then I suppose some statistics are in order. Whiteside is a career 100 percent 3-point shooter. He has made both of his two attempts from deep, no player with that number of attempts has ever shot a higher percentage than Whiteside. In fact, no player has ever shot a better percentage than Whiteside from 3-point range regardless of attempts.

I am joking of course. The precise reason we ignore players with such few attempts from conversations like best shooter of all time is because unlikely outcomes happen with more frequency than they would with larger sample sizes. Few attempts likely do reveal to us something important about a player’s shooting ability — they are suggestive of a player with a poor shooting percentage. A coach is often paid money in order to best put his players in a position to win the game, they do not accomplish this by allowing poor shooters to fire away. This means players unlikely to make a shot are prevented from even attempting to do so, and players likely to make a shot are encouraged to attempt that shot.

Comparing players with a differing number of attempts can be problematic for this reason. Often some cutoff point is assigned, players who have attempted at-least 100 3s for example. However, sometimes we want to include all players in a data-set, selection bias can be an issue for a study.

It is possible to use Bayesian statistics to update a player’s shooting-percentage*. In this case, I will be using the number of 3-point attempts a player has taken to update their 3-point percentage. Their relationship is depicted below.

The method for doing so is (α+3-Point Makes)/(β+ 3-Point Attempts), where α and β are prior parameters set up by regressing 3-point percentage on 3-point attempts. A simple way to look at it is something like this: the average 3-point percentage for all players who have attempted approximately 10 3-pointers is 19 percent then α=19 and β=100. The advantage to this methodology is players who have attempted nine 3-pointers and made all nine will have a slightly improved 3-point percentage over someone who shot nine and missed all of their attempts.

The process is more complicated than the one detailed above, but the idea is similar.

So, what is Whiteside’s updated 3-point percentage? It would be 19 percent — a far cry from Steve Kerr’s career mark of 45 percent. Andrew may have been right after all.

It remains important that the Bayesian parameters not have a large influence on players with a large number of attempts. With a larger sample size we are confident their 3-point percentage is reflective of their ability as a shooter.

Indeed, as the number of attempts increased,  the absolute value of the difference between a player’s actual percentage and their adjusted percentage approaches zero.

One possible application of this Bayesian updating is the prediction of 3-point percentage using college statistics. Instead of adjusting for professional 3-point percentage. I adjusted collegiate percentage using the same method. Collegiate shooting tends to be noisier than its professional counterpart — a product of fewer games in each season, and that better players play fewer seasons.

The trend in the middle percentages, 25 percent to 45 percent, looks like what may be expected. This is quite possibly because players that have shot a significant number of 3s are likely to have a percentage somewhere in that range. The distributions at the extremes look much stranger, and are unlikely to be predictive. Using the updated percentages gives the following distributions.

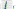
There are still some oddities at the low end, where we expect those with few attempts and thus a noisier percentage to lie, but ultimately the trend looks to be more predictive.

Models used to predict 3-point percentage will often include a player’s collegiate 3-point attempt rate (3PTR) along with their their 3-point percentage. The purpose of 3PTR is similar to that of the Bayes estimation. It is an attempt to capture how comfortable a player is with taking 3s, and how comfortable his coach is with allowing him to shoot. Even if the percentage was not stellar, the player likely showed a high-level of skill in practice, but was simply unlucky in the game. 3PTR is often a significant predictor; however, using only the Bayesian updated college 3-point percentage explained more variance than both non-adjusted 3-point percentage and 3PTR did together.

In addition to adjusted 3-point percentage, I will be using free-throw percentage in college to predict shooting. Often, free-throw percentage is a better predictor than collegiate 3-point shooting. Free throws, without the impediment of a defender or a significant time-constraint, are more reproducible, and better reveal the flaws in a player’s mechanics than a jump shot will.

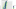
The distribution of shooting percentage tends to tighten as free-throw shooting improves, and the median outcome steadily climbs with improved free-throw shooting. Using the Bayesian adjusted 3-point percentage makes the trend more evident.

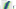
Using Will Schreefer’s data-set I estimated a model using a robust regression. Only players that had played in at-least three NBA seasons were included in the model. The dependent variable was professional 3-point percentage. The independent variables were college free throw percentage, an interaction variable between position and adjusted college 3-point percentage, and an interaction between height and position. There is an interaction between position and adjusted percentage in order to account for possible differences in offensive roles. A center’s percentage may be regressed down due to few attempts, but it may be due to role in college, not lack of skill.

The model had a mean absolute deviation (mae) of 0.08, but the mae was only 0.04 for players with more than 100 3-pointers attempted. The model struggled with those who had only a few attempts, but estimated the percentage for players with a large number of attempts reasonably well.

The results for some notable draft selections from this year are listed below.

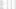
Centers were the story of this year’s draft. Four of the top-seven picks were listed as centers; Jaren Jackson, listed at 6-foot-11, went fourth to Memphis as a power-forward. The top-end talent of the draft may be players that find themselves looking for offense around the rim in a league ever-desperate for more perimeter shooting.

The model loved Jaren Jackson Jr. In fact, all attempts at making this model predicted Jackson to shoot over 40 percent. Deandre Ayton was a bit of a surprise, a possible issue is the interaction between height and position. Centers saw an additional four percent in their shooting for every inch taller they were than the average, the largest effect for any position. The effect may be overstated, but a possible explanation is the center is the tallest position on the floor so being tall for a center means you will be able to easily shoot over any defender. In a similar vein, point-guards see almost no improvement in their shooting based on height.

The other notable centers — Wendell Carter Jr., Marvin Bagley III and Mo Bamba are all projected to shoot poorly from deep. Wendell looks to be a possible miss by the model, he shot 41 percent from 3 in college, and a decent mark from the stripe at 74 percent. Having attempted only 46 3s on the season significantly hurt his adjusted percentage. Bamba has reportedly worked diligently to refine his mechanics, and may have convinced front-offices of the change as the Magic took the center with the sixth pick in the draft. Marvin Bagley… well he’s on the Kings so like…

*If you are interested in learning more about Bayesian statistics, or the statistical-software R, I highly recommend David Robinson’s blog VarianceExplained. I borrowed heavily from it for this post.