Nylon Calculus: Predicting playoff position and probability

The Western Conference standings are a jumbled mess with only five games separating positions No. 4 through No. 10.  In the Eastern Conference, things are not as competitive, except at the top where only six games separate teams No. 1 through No. 5. With about 30 games left for most teams, my goal here is to clear the muddiness of the conference standings by predicting playoff position and probabilities.

In order to estimate the final playoff position, we need a way to estimate wins for each team. To do this I used two useful ideas from math, Bayesian inference and binomial likelihood. A binomial distribution provides us with the likelihood of k successes in n trials of with each trial having only two possible outcomes, success or failure. Binomial trials fit well with basketball games as each game has only two outcomes, either a win or a loss, and we can estimate the probability of winning for any given team. For example, we could calculate the probability a team with a winning percentage of .600  wins six out of the next 10 games by plugging in p=.6, k= 6 and n=10 into the right side of the formula below.

The second useful mathematical idea for this scenario is Bayesian inference. Bayesian inference allows us to continue to make updates to our predictions when new data comes in. In fact, this is the main idea behind Bayesian inference, we use prior information to calculate posterior probabilities and then we can use the posterior probabilities as new prior information when new data comes in.

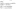
Bayes Theorem is the basis for Bayesian inference and is stated above. Bayes theorem allows us to calculate the probability that our hypothesis is true given the data we have P(H|D). If we know the values on the right side we can calculate the posterior probability.

Assuming the winning percentages are continuous will allow us to look at the continuous version of Bayes theorem instead of the discrete version shown above.  Using the continuous version will let us analyze the distribution of possible outcomes, specifically a beta distribution. A beta distribution offers a good model for the randomness of percentages since the Beta distribution ranges from 0-1. Under these assumptions, our prior distribution will be a beta distribution with parameters a and b, Beta(a, b), and our likelihood will be binomial as described earlier.  Thanks to the idea of conjugate priors, we can assume our posterior distribution will be a beta distribution as well. In our scenario, we will gather data on a number of wins over a period of games and therefore our posterior distribution will be Beta(a + wins since prior, b + losses since prior ). That’s enough math for now but if you would like to know more, the idea for this post came from this Coursera course and this MIT course.

Using the Bayesian process described above we will estimate the winning percentage, and therefore the win totals, for each team using the means of their respective beta distributions.  Our prior win projections will be based on the preseason over/under Vegas win totals from here. We will update our win projections at the halfway point of the season at 41 games played for each team. Finally, we will do another update for games played through Feb. 5. Our final win projections and playoff probabilities will be based on the final posterior distribution.

The process for any single team will look like the graphs below. I chose two of the best performing teams from the East in Milwaukee and Brooklyn as well as two interesting teams in the West, the Rockets and the Clippers. Each image contains the plot of the initial prior distribution, midseason distribution, and each team’s final distribution as well as the expected number of wins for each time frame.

Houston Bayes Detail

Milwaukee Bayes Detail

Clippers Bayes Detail

Brooklyn Bayes Detail

We can see that both the Bucks and Nets continue to play above expectations and have improved their expected win totals by nearly 10 wins for the Bucks and over six wins for the Nets. The Rockets, on the other hand, have decreased their expected win total by almost four due to underperforming compared to preseason expectations. The most interesting team here is the Clippers. While they performed well in the first half of the season, they have dropped off lately and are seeming to regress to a lower level of performance.

Using the same process for all teams, we can predict playoff positioning by grouping them by conference and sorting them by the final projected mean. The graph below shows the projected playoff positioning for each team based on their preseason prior in blue, midseason update in red, and their final update on Feb. 5 in green.

As we can see from the plot above we have the top eight projected teams in the West including the Lakers (LAL) and all teams above them. Similarly, in the East, we have Charlotte and everyone above. Some interesting outcomes here come mostly from the surprisingly successful teams. Milwaukee, Brooklyn, LA Clippers and Sacramento are all projected to finish lower in the standings than their current position. This is mostly due to their initial priors being significantly lower than their current performance. Will these teams regress as the model suggests or can they maintain their stellar performance for a full 82 game schedule? We can already see that the Clippers have started to regress to their actual expected wins since their midseason peak.

Win projections are great but I also was curious as to the probability of each team making the playoffs. We will use each team’s final beta distribution and the lowest projected win total of the eighth seed in each conference to estimate each team’s playoff probability. In the West, the lowest playoff win total is 44 games while in the East it is a measly 38. The plot below shows the probability of making the playoffs for each team based on their final distributions and the minimum number of wins required to make the playoffs.

This model seems to suggest that maybe the Western Conference isn’t as competitive as I thought. There are a lot more good teams in the West but the top eight teams have a much higher probability than any of the remaining seven teams.  In the Eastern Conference, there are a lot more teams that have at least some chance of making the playoffs. It will be interesting to see how Detroit, Charlotte, Brooklyn, Washington, and Miami battle it out for the final three playoff spots.

Using this Bayesian process we are able to come up with predictions of win totals and playoff probabilities. There are some major drawbacks here mostly due to assuming winning percentage will be the same for each game regardless of location or opponent. Teams with more home games or more games against sub .500 teams will have prettier projections until they start playing tougher games. Also, this model doesn’t take into account any of the current changes due to trades or injuries. Once the trade deadline passes team rosters will be more solidified and provide a better idea as to how the team will perform going forward. The great thing about using Bayesian inference is we can continually update our projections as new information comes in, eventually leading to more accurate predictions.

With the competitiveness between the top teams, it might come down to the last few weeks or days of the season until we get a solid understanding of where teams will be positioned. As the season wears on each game will become increasingly important and will make for an entertaining final few months of the NBA season. I will enjoy watching these teams shoot it out as they jockey for playoff positioning.

Win totals and record data provided by basketball-reference.com