Nylon Calculus: What’s the right number of 3-pointers to attempt?

In my last post, I outlined a generalized model for determining the optimal shot distribution for a team. The main assumption underlying the model was that a shot’s quality was a function of its frequency. I briefly touched on another assumption as well.

"The final piece of the graph is the straight line that runs from axis to axis. This is the budget constraint. The slope of the budget constraint is described by the costs of the two inputs. Luckily, the cost of both inputs is the same, taking one more of either shot simply costs a shot, therefore the slope of the budget constraint is 1."

That assumption — that the cost of all shot types are equal, or, more correctly, that the pursuit of different strategies all have the same costs — makes the model easy, the math clean. It is, however, not true. The pursuit of certain shots is simply more likely to lead to turnovers, and rebounding rates are not constant across shot types.

Keeping with the simplified model of choosing between 2s and 3, and using pbpstats’s shot location and free-throw source statistics, both per-100 possessions, for the last five seasons we can visualize the trade-off in scoring opportunities between the two shot types — the slope is written just to the right of the constraint.

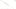
If the costs of pursuing 2s and 3s were equal we would expect a slope of -1. The slope of the constraint here is -1.07. The effect sounds small, but if a team pursues a strategy of only shooting 3-pointers over the course of 100-possessions they would be expected to have 6.4 fewer scoring opportunities than they would if they only shot twos. Using league averages for 2 and 3-point percentage from last-season the team attempting only 2-pointers would be expected to outscore the team attempting only 3s given this budget constraint, just barely — 99.9 points per-100 to 99.4. Revisiting the example model set up in the previous post, we can explore how the updated budget constraint changes the equilibrium.

• Expected PPS for 3-pointers=1.2-.0025x
• Expected PPS for 2-pointers=1-.005y
  • Where y is equal to the total number of shots available minus threes
• The slope of the isoquant is (1.2-.005x)/(1-.001y)
• Total points = X(1.2-.0025x)+Y(1-.0005y)

There is one change to the example aside from the budget constraint’s slope. The total number of shots to be allocated is set to 98, the estimated number of scoring opportunities a team would have if they only took 2s. For an easier comparison, assuming the slope of the budget constraint was in fact -1, then the optimal number of 3-pointers with only 98 shots to allocate would be 49.67.

The setup to the problem with the new budget constraint is

[(1.2-.005x)/ (1-.001y)]=1.07

That is, the slope of the isoquant is equal to the slope of the budget constraint — the tangency condition. The optimal number of 3s to attempt under this condition reduces to 38.2, and the number of 2-pointers increases to 57.1. That 3s tend to be a little more “costly” helps explain why we rarely see teams with massive 3-point attempt rates.

Of course, framing the decision as 3s vs 2s is not entirely accurate either. A team’s shot selection can be divided into five sections: at the rim, short mid-range, long mid-range, corner 3, and above-the-break 3 — Justin Jacobs recently introduced a far more interesting and nuanced approach to defining shot types here.

If the cost of each shot type were the same — if neither likelihood of a turnover nor the chance of getting a rebound following a miss differed, only the area on the floor —  the slope of the constraint should be  -1. Anything above that would mean that a strategy that emphasized that shot would net more shots per-100, and anything below implies that a strategy emphasizing that shot would net fewer shots per-100 either due to associated turnover or rebounding rates.

What we find is that a large portion of the additional cost of pursuing 3s comes from pursuing corner 3s. The corner 3 is a valuable tool as it is a few feet closer to the rim than 3s from above the break, and is generally more open. Over the previous five seasons, teams collectively made 39 percent of their shots from the corner, compared to just under 35 percent from above-the-break. The cost, though, goes some way to offset the value, making it difficult to put a strong emphasis on shooting from the corner.

Conversely, mid-range shots have low costs relative to the other shot areas. Even so, given the low value of 2-point jump shots, pursuing an offensive strategy heavy on mid-range attempts is unlikely to net an efficient offense. Excluding outliers in skill, an offense’s optimal shot-distribution is likely to include some mid-range shots given that they are easy to come by and can operate as a reasonable bail-out, but few as 3-pointers and attempts at the rim are far more valuable as first options.

The costs associated with offensive strategies are a key component in determining the optimal scheme. Relying heavily on shots that your team simply cannot conjure, even if they are very valuable, is not a sustainable practice. The budget constraint helps illuminate this concept — that is why I chose a graph with it when explaining the model. With an additional touch of reality, the model can begin to explain why teams cannot blindly pursue only high efficiency looks at the rim and from behind the 3-point line. That is, unless that team happens to have two generational isolation scorers and distributors; that offense might just operate unconstrained.